Notion de suite
Généralités
Une suite numérique est une fonction définie pour tout entier \(n\in\mathbb{N}\) et à valeurs dans \(\mathbb{R}\) $$u:\begin{array}{rcl} \mathbb{N}&\longrightarrow&\mathbb{R}\\ n& \longmapsto &u(n) \end{array}$$ On note en général \(u_n\) l’image de \(n\) par la suite \(u\), également appelé terme de rang \(n\).
La suite \(u\) est également notée \((u_n)_{n\in\mathbb{N}}\) ou \((u_n)\)
Exemple : On peut définir la suite \((u_n)\) des nombres impairs. On a alors \(u_0=1\), \(u_1=3\), \(u_2=5\)…
Comme pour les fonctions, on peut définir une suite à l’aide d’une formule explicite.
Exemple : On considère la suite \((u_n)\) telle que, pour tout \(n\in\mathbb{N}\), \(u_n=3n+4\). On a alors :
- \(u_0=3\times 0 + 4 = 4\)
- \(u_1=3\times 1 + 4 = 7\)
- \(u_2=3\times 2 + 4 = 10\)…
Suite définie par récurrence
On dit qu’une suite \((u_n)\) est définie par récurrence (d’ordre 1) lorsqu’il existe une fonction \(f:\mathbb{R}\to \mathbb{R}\) telle que, pour tout \(n\in\mathbb{N}\), \(u_{n+1}=f(u_n)\). Autrement dit, tout terme de la suite se construit à partir du terme précédent.
Exemple : On définit la suite \((u_n)\) comme suit :
- \(u_0=-2\)
- pour tout \(n\in\mathbb{N}\), \(u_{n+1}=u_n^2+3\)
On a ainsi
- \(u_1=u_0^2+3=(-2)^2+3=7\)
- \(u_2=u_1^2+3=7^2+3=52\)
- \(u_3=u_2^2+3=52^2+3=2707\)
Cliquer ici pour s’entraîner : Calcul de termes de suites
Représentation graphique
On se place dans un repère \((O;\vec{i};\vec{j})\). La représentation graphique d’une suite \((u_n)\) est l’ensemble des points de coordonnées \((n:u_n)\) pour \(n\in\mathbb{N}\).
Exemple : Cet exemple utilise des notions du chapitre Trigonométrie.
On considère la suite \((u_n)\) telle que, pour tout \(n\in\mathbb{N}\), \(u_n=\cos\left( \dfrac{n\pi}{2} \right)+n\).
- \(u_0=\cos (0)+0=1\), on place le point de coordonnées \((0;1)\).
- \(u_1=\cos \left(\dfrac{\pi}{2}\right)+1=1\), on place le point de coordonnées \((1;1)\).
- \(u_2=\cos \left(\pi\right)+2=1\), on place le point de coordonnées \((2;1)\)…

Sens de variation d’une suite
Variations d’une suite
Soit \((u_n)\) une suite numérique et \(n_0\in\mathbb{N}\)
- On dit que \((u_n)\) est croissante à partir du rang \(n_0\) si, pour tout \(n\geqslant n_0\), \(u_n\leqslant u_{n+1}\).
- On dit que \((u_n)\) est décroissante à partir du rang \(n_0\) si, pour tout \(n\geqslant n_0\), \(u_n\geqslant u_{n+1}\).
- On dit que \((u_n)\) est constante à partir du rang \(n_0\) si, pour tout \(n\geqslant n_0\), \(u_n= u_{n+1}\).
Comme pour les fonctions, il existe des strictes croissances et décroissances de suite
Exemple : Soit \((u_n)\) la suite définie pour tout \(n\) par \(u_n=2n^2+5n-3\). Soit \(n\in\mathbb{N}\)
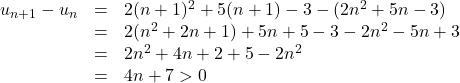
Ainsi, pour tout \(n\in\mathbb{N}\), \(u_{n+1}-u_n>0\), c’est-à-dire \(u_{n+1}>u_n\). La suite \((u_n)\) est donc strictement croissante (à partir du rang \(0\)…).
Soit \((u_n)\) une suite dont les termes sont tous strictement positifs et \(n_0\in\mathbb{N}\).
- \((u_n)\) est croissante à partir du rang \(n_0\) si et seulement si, pour tout \(n\geqslant n_0\), \(\dfrac{u_{n+1}}{u_n}\geqslant 1\).
- \((u_n)\) est décroissante à partir du rang \(n_0\) si et seulement si, pour tout \(n\geqslant n_0\), \(\dfrac{u_{n+1}}{u_n}\leqslant 1\).
Exemple : Soit \((u_n)\) la suite définie pour tout \(n\in\mathbb{N} \setminus \{0\}\) par \(u_n=\dfrac{2^n}{n}\).
- Pour tout \(n\in\mathbb{N}\), \(u_n>0\)
- Pour tout \(n\in\mathbb{N}\), \(\dfrac{u_{n+1}}{u_n}=\dfrac{2^{n+1}}{n+1}\times \dfrac{n}{2^n}=\dfrac{2n}{n+1}\)
Or, pour tout \(n>1\), on a \(n+n>n+1\), c’est-à-dire \(2n>n+1\), soit \(\dfrac{2n}{n+1}>1\).
Ainsi, pour tout \(n>1\), \(\dfrac{u_{n+1}}{u_n}>1\). La suite \((u_n)\) est donc croissante à partir du rang 1.
Lien avec les fonctions
Soit \(n_0\in\mathbb{N}\) et \(f\) une fonction définie sur \(\mathbb{R}\) et monotone sur \([n_0;+\infty[\).
La suite \((u_n)\), définie pour tout \(n\in \mathbb{N}\) par \(u_n=f(n)\), est monotone à partir du rang \(n_0\), de même monotonie que \(f\).
Puisque \(n\leqslant n+1\), alors, par croissance de \(f\) sur \([n_0;+\infty[\), \(f(n)\leqslant f(n+1)\), c’est-à-dire \(u_n\leqslant u_{n+1}\). La suite \((u_n)\) est donc croissante à partir du rang \(n_0\).
La démonstration est analogue si \(f\) est décroissante.La réciproque est fausse ! La suite \(\left(\cos\left(\dfrac{n\pi}{2}\right)+n\right)\) est croissante, mais la fonction \(x\mapsto \cos \left( \dfrac{x\pi}{2}\right)+x\) n’est pas monotone
Limites de suite
En classe de Première générale, le programme se limite à une approche intuitive de la limite. Celle-ci sera davantage développée en classe de Terminale pour les chanceux qui continueront les mathématiques.Limite finie
Soit \((u_n)\) une suite numérique.
On dit que la suite \((u_n)\) converge vers 0 si les termes de la suite « se rapprochent aussi proche que possible de 0 » lorsque \(n\) augmente.
On dit que 0 est la limite de la suite \((u_n)\) en \(+\infty\), ce que l’on note \(\lim\limits_{n\to +\infty}u_n=0\)
Exemple : On considère la suite \((u_n)\) définie pour tout \(n>0\) par \(u_n=\dfrac{1}{n}\) \(u_1=1\) , \(u_{10}=0.1\) , \(u_{100}=0.01\) , \(u_{100000}=0.00001\)…\\ La limite de la suite \((u_n)\) en \(+\infty\) semble être 0. On peut l’observer sur la représentation graphique de la suite.

Soit \(a\) et \(b\) deux réels avec \(a\neq 0\). La suite \(\left(\dfrac{1}{an+b}\right)\) converge vers 0.
Soit \(L\) un réel et \((u_n)\) une suite numérique.
On dit que la suite \((u_n)\) converge vers \(L\) si les termes de la suite « se rapprochent autant que possible de \(L\) » lorsque \(n\) augmente.
Soit \(L\) un réel et \((u_n)\) une suite numérique.
Le suite \((u_n)\) converge vers \(L\) si et seulement si la suite \((u_n-L)\) converge vers 0.
Exemple : On considère la suite \((u_n)\) définie pour tout \(n\in\mathbb{N}\) par \(u_n=\dfrac{6n-5}{3n+1}\). On représente graphiquement cette suite dans un repère orthonormé.

Il semble que la suite se rapproche de la valeur 2. Notons alors \((v_n)\) la suite définie pour tout \(n\in\mathbb{N}\) par \(v_n=u_n-2\)
Pour tout \(n\in\mathbb{N}\), \[v_n=u_n-2=\dfrac{6n-5}{3n+1}-2=\dfrac{6n-5}{3n+1}-\dfrac{6n+2}{3n+1}=\dfrac{-7}{3n+1}\] Ainsi, \((v_n)\) converge vers 0, donc \((u_n)\) converge vers 2.
Limite infinie
Soit \((u_n)\) une suite numérique.
On dit que la suite \((u_n)\) tend vers \(+\infty\) si \(u_n\) devient « aussi grand que l’on veut et le reste » lorsque \(n\) augmente. On note \(\lim\limits_{n\to +\infty}u_n=+\infty\)
Exemple : On considère la suite \((u_n)\) définie pour tout \(n\) par \(u_n=n^2\).
\(u_0=0\), \(u_{10}=100\), \(u_{100}=10000\), \(u_{1000}=1000000\)… La suite semble tendre vers \(+\infty\).
Prenons en effet \(A\in\mathbb{R}+\). Alors, dès que \(n\geqslant \sqrt{A}\), on a \(u_n=n^2\geqslant A\), par croissance de la fonction Carré sur \(\mathbb{R}+\). Ainsi, \(u_n\) devient plus grand que n’importe quel nombre, à partir d’un certain rang.



